조합과 순열 Feat. JavaScript

 

📌 조합

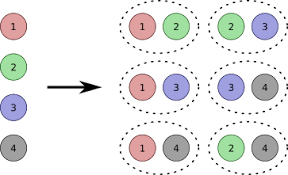
서로 다른 n개의 원소를 가지는 어떤 집합에서 순서에 상관없이 r개의 원소를 선택하는 것입니다. 기호로 나타내면 nCr 입니다.
예를 들어, 4C3를 직접 구해서 써본다면 아래와 같이 나옵니다.

Input: [1,2,3,4]
Output: [[1,2,3],[1,2,4],[1,3,4],[2,3,4]]

예시에서 볼 수 있듯이, 조합은 순서를 상관하지 않습니다. ( [1,2,3] = [3,1,2] )
내부의 숫자가 같다면 그냥 같은 것으로 칩니다.

---

💦 풀이 과정

배열에서 순서대로 하나씩 선택하고, 나머지 원소들로 조합을 합니다.
나머지 원소들로 조합을 할때는 재귀를 사용하면 편합니다.

예시)
[1,2,3,4]
선택 [1], 나머지 [2,3,4]에서 2개를 조합히면 [1,2,3],[1,2,4],[1,3,4]
선택 [2], 나머지 [3,4]에서 2개를 조합하면 [2,3,4]
선택 [3], 나머지 [4]에서 2개를 조합하면 []
선택 [4], 나머지 []에서 2개를 조합하면 []

 

---

📄 코드 구현

const Combination = (arr, num) => {
    const result = [];

    if (num === 1) return arr.map(v=>[v]);
    // 하나를 선택하게 되면 모든 원소를 리턴

    arr.forEach((select, i, origin)=>{
        const remainder = origin.slice(i+1);
        // 선택한 숫자 뒤부터 저장 => 나머지
        const combination = Combination(remainder, num-1);
          // 재귀로 숫자를 줄여가며 조합
        const combine = combination.map(v=>[select, ...v]);
          // 선택한 숫자와 조합된 배열들을 합침
        result.push(...combine);
          // 결과 배열에 조합된 배열들 모두 저장
    });

    return result; // 결과 리턴
}

 

---

📌 순열

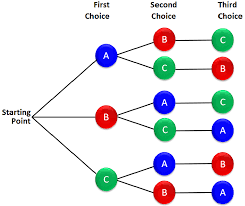
서로 다른 n개의 원소에서 r개를 중복 없이 순서에 상관있게 선택하는 혹은 나열하는 것입니다. 기호로 나타내면 nPr 입니다.
예를 들어, 3P2를 직접 구해서 써본다면 아래와 같이 나옵니다.

Input: [1,2,3]
Output: [[1,2],[1,3],[2,1],[2,3],[3,1],[3,2]]

순열은 조합과는 다르게 순서가 상관이 있습니다. ( [1,2] != [2,1] )

 

---

💦 풀이 과정

전체적으로 구현하는 것은 조합과 유사하지만 한 부분이 다릅니다.

const remainder = [...origin.slice(0,i), ...origin.slice(i+1)];
          // 선택한 숫자의 앞 숫자들과 선택한 숫자의 뒷 숫자들을 합쳐준다.

조합은 순서가 상관 없기 때문에 하나를 선택하면 선택한 숫자의 앞 숫자는 뒤로 들어가지 않지만,

순열은 순서가 상관이 있기 때문에 선택한 숫자의 앞 숫자도 뒤에서 다시 등장할 수 있습니다.

예시
조합
[1,2,3,4] => 1 선택 => [2,3,4] => 2 선택 => [3,4] => 3 선택 => [4]
                                                        => 4 선택 => [3]
                                                끝
순열
[1,2,3,4] => 1 선택 => [2,3,4] => 2 선택 => [3,4] ~
                                 => 3 선택 => [2,4] ~
                              => 4 선택 => [1,4] ~

 

---

📄 코드 구현

const Permutation = (arr, num) => {
    const result = [];

    if (num === 1) return arr.map(v=>[v]);

    arr.forEach((select, i, origin) => {
        const remainder = [...origin.slice(0,i), ...origin.slice(i+1)];
          // 선택한 숫자의 앞 숫자들과 선택한 숫자의 뒷 숫자들을 합침
        const permutation = Permutation(remainder, num-1);
        const combine = permutation.map(v=>[select, ...v]);
        result.push(...combine);
    });

    return result;
}